
Some times ago I bought the motherboard BC3486UL Rev. 1.2 (manufacturer is unknown) which has a combined 486 / 387 socket and a separated 386 socket. The same board can handle:
- one 386 CPU plus mathematical co-processor or
- one 486DLC (486 core in a 386 housing) plus mathematical co-processor or
- one 486 CPU
Jumper settings aren't a problem because I got the board with the manual.
This board allows me to measure and compare the performance of the well known: AMD Am386DX, Cyrix 486DLC and a "full" 486 (AMD Am486DX) in the same environment.

All CPU's run with 40MHz. I don't own all processors with a 40MHz speed rating but I didn't see any problems by "overclocking" 33MHz types for a short time.
I was additional interested in the performance of some mathematical co-processors:
- IIT 3C87
- IIT 4C87DLC
- Cyrix FasMath 83C87
- ULSI US83C87-C
- and the internal implementation of AMD 486DX
All measurement results are documented here.
AMD Am386DX-40 - still a legend
This processor was the first one and got the privilege to be the reference CPU.
He delivers a Dhrystone2 value of 17410 - not bad for a cacheless processor with only 275000 transistors...
Cyrix 486DLC-40GP - a 486 in the 386's clothing
The processor was intended to upgrade 386 computers to 486 performance without generate a lot of electronic waste and, clearly, save a lot of money.
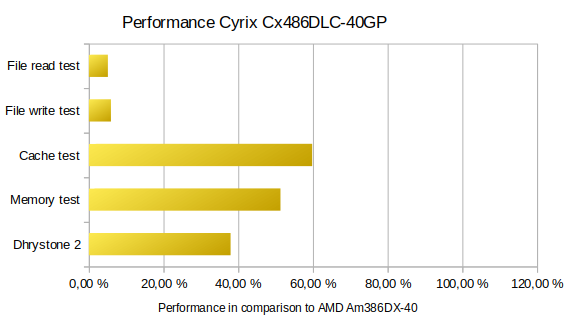
Nearly 40% more integer performance and a significant increased memory throughput - this processor gave the old 386 hardware a proper performance boost.
AMD 486DX-40 - a real 486
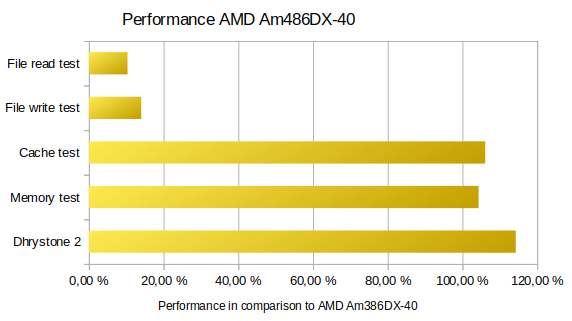
No doubts - this processor has twice the performance of its 386 sister at the same clock speed (so as mentioned on Wikipedia).
Mathematical co-processors - the best friends of the CPU

Cyrix FasMath processors enjoy a high reputation - and rightly so: it calculates over 50% faster than IIT. But also the ULSI chip is a good choice. It has the same performance as Cyrix FasMath.
But the external co-processors have no chance against an integrated floating point unit - AMD 486DX calculates twice as fast as Cyrix FasMath or ULSI.
falk.richter*at*yandex.com
Last update: March 12, 2020